NeRF. Представление сцен в виде нейронных полей излучения для синтеза изображений
В данной статье предложен метод, который позволяет по набору снимков, получать новые изображения той же сцены из точек, для которых в исходном наборе не было фотографий. Для этого тренируется нейронная сеть, которая для каждой трехмерной точки сцены с координатами $(x, y, z)$ для направления $(\theta, \phi)$ восстанавливает “прозрачность” этой точки и излучение в нужном направлении. Такое представление сцены авторы называют neural radiance field (NeRF)

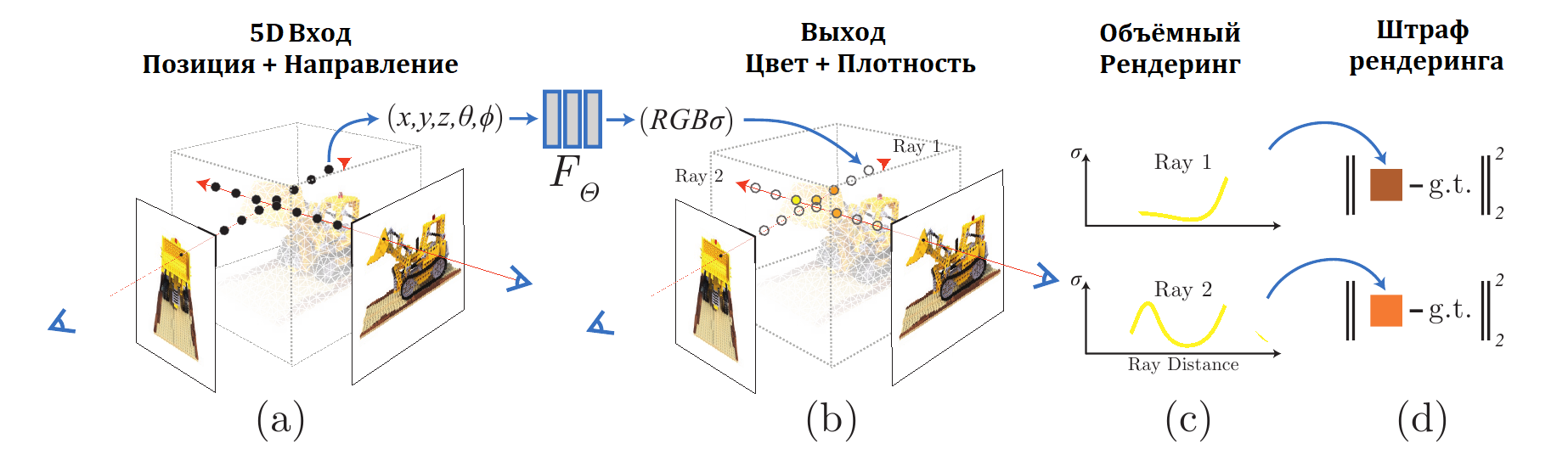
Итак трёхмерная сцена представляется в виде нейронной сети, которая преобразует 5-мерные координаты $(x, y, z, \theta, \phi)$ в “прозрачность” данной точки и RGB цвет. Чтобы получить из этого представление сцены изображение для камеры, расположенной в определенной точке используется следующая процедура:
- из камеры выпускаются лучи через сцену. На каждом луче генерируется множество трехмерных точек
- для каждой точки на луче и соответствующего направления нейронная сеть выдаёт цвет и прозрачность
- далее используется классическая техника объемного рендеринга, чтобы получить двумерную картинку
Все этапы данного алгоритма дифференцируемы, а значит можно, используя имеющиеся изображения и градиентные методы оптимизации, натренировать сеть. Заметим, что для каждой трехмерной сцены необходимо тренировать свою сеть (что вполне естественно).
Итак нужно натренировать сеть, которая получает на вход трехмерные координаты $(x, y, z)$ и направление луча (вместо двух углов, авторы задают направление при помощи единичного вектора $d$). На выходе сеть должна выдать цвет $c = (r, g, b)$ и плотность-прозрачность $\sigma$.
Т.е. нужно получить представление непрерывной функции $F_{\Theta}: (X, d) \rightarrow (c, \sigma)$ в виде нейронной сети с весами $\Theta$. Для этого авторы предлагают вначале преобразовать трехмерные координаты точки сетью из 8 полносвязных слоёв (с ReLU в качестве нелинейности и 256 каналами на каждом слое) получив на выходе $\sigma$ и вектор особенностей размерности 256. Затем расширить вектор особенностей, добавив вектор направления луча и прогнать, получившийся вектор через еще один полносвязный слой (размерности 128, и тоже с ReLU) получив на выходе цвет.
Авторы отмечают, что если не использовать направление луча, а подавать на вход только координаты точки, то возникают проблемы с бликами:

Рассматривая $\sigma(X)$ как плотность вероятности того, что луч остановится в точке $X$, можно получить цвет $C(r)$ в точке на изображении, соответствующей лучу $r(t) = o + td$, где $t$ изменяется от $t_n$ до $t_f$. Для этого используется следующая пара формул:
\[\begin{align*} C(r) &= \int_{t_n}^{t_f} T(t)\sigma(r(t))c(r(t), d) dt,\\ T(t) &= \exp\left(-\int_{t_n}^{t} \sigma(r(s)) ds \right) \end{align*}\]Функция $T(t)$ обозначает вероятность, что луч пройдя от $t_n$ до $t$ не затронет частиц в точках на своём пути (и значит не остановится).
Замечание. Авторы в списке литературы указывают работу Max, N.: Optical models for direct volume rendering. IEEE Transactions on Visualization and Computer Graphics (1995). Мне пригодилось прочитать, чтобы понять откуда берутся формулы и какие численные методы применяются.
Чтобы сгенерировать изображение на основе NeRF надо уметь вычислять интеграл $C(r)$ вдоль луча для каждого пикселя камеры для которой мы генерируем изображение. Для этого отрезок $[t_n, t_f]$ делится на $N$ равных частей, после чего, вообще говоря, в зависимости от метода численного взятия интеграла, предполагается брать какую-то фиксированную точку в каждой части отрезка (начальную, среднюю, …), но если так делать, то и сеть будет втренировываться на фиксированные точки, поэтому точки внутри частей выбираются случайным образом (равновероятно):
\[t_i \in \left[t_n + \frac {i-1} N (t_f - t_n), t_n + \frac i N (t_f - t_n) \right], \, i=1,2,...,N\]обозначая $\delta_i = t_{i+1} - t_i$ получаем:
\[\begin{align*} \tilde C (r) &= \sum_{i=1}^N T_i \left(1 - \exp(-\sigma_i \delta_i)\right) c_i\\ T_i &= \exp\left(- \sum_{j=1}^{i-1} \sigma_j \delta_j \right) \end{align*}\]Однако, авторы говорят, что попытка просто натренировать функцию на пяти координатах приводит к не особо хорошим результатам, качество получаемых при этом картинок низкое. Чтобы получить более качественные результаты, они предлагают передавать не просто координаты точек, а их же, но модулированные высокой частотой, т.е. на вход сети вместо $(x, y, z)$ предлагается передать $(\gamma(x), \gamma(y), \gamma(z))$, где
\[\gamma(u) = \left(\sin\left(2^0\pi u\right), \cos\left(2^0\pi u\right), ..., \sin\left(2^{L-1}\pi u\right), \cos\left(2^{L-1}\pi u\right) \right), \, u \in [-1, 1]\]$(x, y, z)$ предварительно нормализуются к отрезку $[-1, 1]$.
Аналогично модулируются и координаты вектора направления $d$.
Авторы используют $L = 10$ для пространственных координат и $L = 4$ для направления. Таким образом вход сети вместо $\mathbb R^5$ превращается в $\mathbb R^{3 \cdot 2 \cdot 10 + 2 \cdot 2 \cdot 4} = \mathbb R^{76}$
Чтобы повысить эффективность работы (просто набирать точки относительно равномерно на луче не очень эффективно, потому что в этом случае точки набираются с той же плотностью и в пустом пространстве, и в загороженной области) авторы предлагают тренировать сразу две сети “грубую” и “точную”.
Вначале на луче набирают $N_c$ точек равномерно и вычисляют в этих точках цвет и “плотность” при помощи “грубой” сети. Сумму для получения цвета можно переписать в виде:
\[\tilde C_c (r) = \sum_{i=1}^{N_c} \omega_i c_i, \, \omega_i = T_i \left(1 - \exp(-\sigma_i \delta_i)\right)\]если нормализовать веса в этой сумме $\tilde \omega_i = \omega_i / \sum_{i=1}^{N_c} \omega_i$, то мы получим плотность дискретного распределения, и логично брать больше точек из областей где эта плотность больше. Так и делается, набирается еще $N_f$ точек на том же луче только теперь уже в соответствии с плотностью полученного распределения. Объединяя оба набора точек прогоняем их через “точную” сетку и, наконец, получаем результирующий цвет $\tilde C_f (r)$, с использованием всех $N_c + N_f$ точек.
Штрафная функция, используемая для тренировки, это просто сумма квадратичных ошибок предсказанных цветов:
\[\mathcal L = \sum_{r} \left( \left| \left| \tilde C_c (r) - C(r) \right| \right|_2^2 + \left| \left| \tilde C_f (r) - C(r) \right| \right|_2^2 \right)\]$C(r)$ это RGB цвет соответствующей точки в изображении из датасета. Авторы используют $N_c = 64$ и $N_f = 128$.
Авторы опубликовали код с использованием TensorFlow: ссылка