CVPR’06

Это базовая статья 2006 года по contrastive loss.

В статье решается задача представления многомерных данных (например, изображений) на многообразии малой размерности. Для этого авторы конструируют новый метод, который они назвали Dimensionality Reduction by Learning an Invariant Mapping (DrLIM), заявляя для этого метода следующие свойства:

1. Для применения метода достаточно только знать для каждой точки тренировочного датасета её “соседей” (это может быть как близость по некоторой метрике в исходном пространстве откуда берутся тренировочные данные, так и ручная разметка пар сэмлов)

2. Функция, которая получается в результате может быть применена не только к данным из исходного датасете, но и к данным того же типа, которые она никогда не видела (при этом для них у нас нет никакой разметки “соседей” из тренировочного набора)

3. Метод может выучивать функцию, которая будет инвариантна к определенным изменениям входных данных таким как, геометрические искажения или изменения освещенности

п.1 важен, потому что мы именно, что хотим иметь представление близости, которая не завязана на близость по какой-то метрике в пространстве исходных данных, а задётся нами по более сложному правилу, возможно размечается вручную.

Формально задача ставится следующим образом. Допустим, у нас есть набор данных ${\cal I} = \{X_i | X_i \in \mathbb{R}^D, i=1,…,N\}$, причем для каждого $X_i \in {\cal I}$ определено подмножество его “соседей” $S_{X_i} \subset {\cal I}$. Мы хотим построить функцию $G_W: \mathbb{R}^D \rightarrow \mathbb{R}^d$, которая бы удовлетворяла следующим требованиям:

а) Размерность $d \ll D$

б) Метрика на результирующем многообразии (например, евклидова) должна соответствовать отношению “соседства” на исходных данных. Т.е. образы соседей должны быть близки в $\mathbb{R}^d$ и наоборот, образы точек, которые не были соседями в исходном пространстве, должны находится на значительном расстоянии в $\mathbb{R}^d$

$G_W$ - предлагается брать как некую нелинейную функцию (в статье все примеры это нейронные сети), параметризованную набором весов $W$, и подбирать эти веса таким образом, чтобы в результате $G_W$ удовлетворяла пункту б) требований.

Тренировка (подбор весов) осуществляется стандартными градиентными методами, достаточно определить штрафную функцию:

\[{\cal L}(W) = \sum_{i=1}^{P} L\left(W, (X_1, X_2, Y)^{(i)}\right)\]

суммирование идет по датасету набранному из пар элементов из ${\cal I} \times {\cal I}$. Метка $Y$ равна $0$, если $X_1$ и $X_2$ соседи, и равна $1$

• если нет.

\[L\left(W, (X_1, X_2, Y)\right) = (1 - Y) L_S(D_W(X_1, X_2)) + Y\, L_D(D_W(X_1, X_2))\]

$D_W(X_1, X_2) = \left\| G_W(X_1) - G_W(X_2) \right\|$ - просто расстояние между образами, а $L_S$ и $L_D$ - штрафы на это расстояние для “соседей” и не “соседей”:

\[L_S(D_W) = \frac 1 2 (D_W)^2\] \[L_D(D_W) = \frac 1 2 \left(\max\{0, m - D_W\}\right)^2\]

$m$ - здесь это гиперпараметр, если для образа данной точки в ее окрестности радиуса $m$ попадает образ “несоседней” точки, то эта пара отталкивается друг от друга (в смысле веса $W$ функции $G_W$ изменяются так, чтобы образы точек разъехались). При этом “несоседние” точки образы которых находятся на расстоянии больше $m$ не оказывают влияния друг на друга.

Слагаемое $L_D(.)$ и использование “несоседей” необходимы при тренировке, чтобы получить хороший результат, иначе можно просто выбрать $G_W = const$

Эксперименты

Авторы берут MNIST и набирают из него для тренировки по 3’000 картинок цифры “4” и цифры “9”, еще по 1’000 картинок этих цифр они откладывают для тестирования.

В качестве, $G_W$ используется сверточная нейронная сетка с двумя сверточными слоями (напомню, что статья 2006 года, так что сетки еще без особых изысков), которая проецирует исходные изображения в пронстранство размерности два.

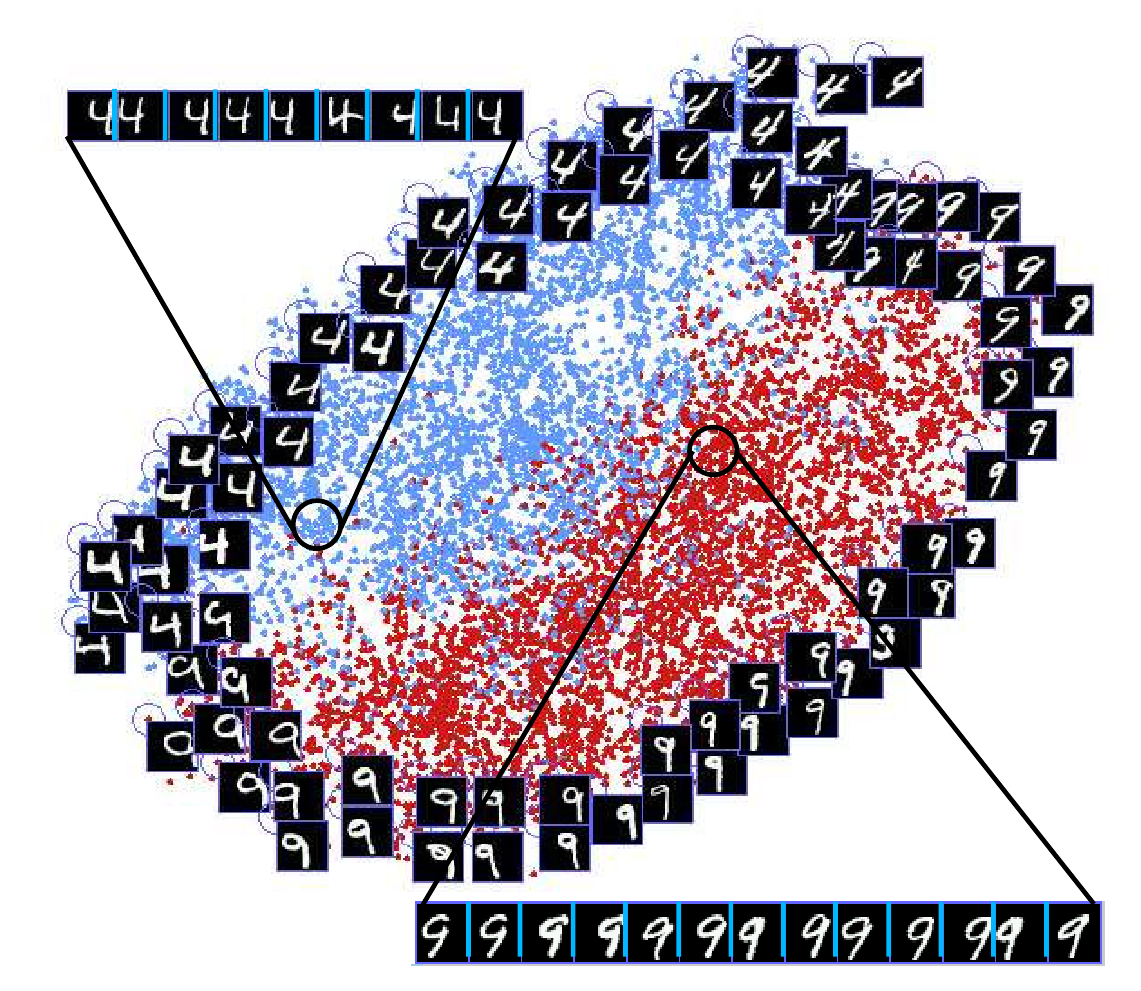
В первом эксперименте, авторы считают соседями пять ближайших по обычной эвклидовой метрике (в пространстве картинок). В результате, на тестовых данных картина выглядит так:

здесь синие точки это изображения цифры “9”, а красные - цифры “4”. Несмотря на очень упрощенный способ определять соседей на исходных данных, очевидно, что представление выделило некую структуру, которая отделяет классы, хотя имеем и достаточно большую область, где равномерно присутствуют образы точек обоих классов.

Для второго эксперимента, авторы каждое изоражение в тренировочном и тестовом датасете, сдвигают по горизонтали на -6, -3, 3, 6 пикселей.

Таким образом тренировочный датасет вырастает до 30’000 изображений, а тестовый до 10’000.

В качестве соседних снова выбирается пять ближайших по эвклидовому расстоянию. Результат представлен на картинке:

Данные разъехались на пять различимых кластеров (по количеству сдвигов), в каждом кластере при этом снова хорошо выделяется структура разных классов.

Наконец, в третьем эксперименте, берутся те же данные, что и во втором, но при этом соседство определяется не просто по близости, но с использованием наших дополнительных знаний, а именно, для изображения соседями считаются:

i. как обычно пять ближайших по евклидову расстоянию между картинками

ii. четыре изображения, полученных сдвигом данного по горизонтали

iii. каждые четыре изображения, полученные сдвигом изображений из п. i.

В результате на тестовом наборе получаем следующую картину:

Видно, что получилось представление инвариантное к сдвигу, и мы уже не наблюдаем те пять кластеров, которые имели место во втором эксперименте.

При этом сдвинутые изображения попадают в близкие точки на многообразии, что логично.