arXiv:1603.08511

Статья про то как раскрашивать черно-белые изображения. Очевидно, что никакого однозначного решения тут нет, т.е. трава обычно зеленая, а небо голубое, но, например, машина может быть практически любого цвета хоть желтого, хоть розового. Часто задачу раскрашивания решают в полуавтоматическом режиме, т.е. человек “натыкивает” точки с цветами, а алгоритм продолжает эти цвета на всё изображение. Авторы предлагают полностью автоматическое решение.

И до этой статьи были подходы к автоматическому решению, которое бы сразу по изображению в градациях серого восстанавливало цвета. Однако, авторы статьи указывают на то, что обычно все такие решения выдавали слишком приглушенные цвета, и в своей статье они в том числе предлагают способ борьбы с этим недостатком.

Большой плюс этой задачи, что можно собрать очень большой тренировочный датасет, причем не потратив ни копейки на разметку. Действительно, просто собираем датасет из цветных изображений и обесцвечиваем. Авторы предлагают делать это используя цветовое пространство Lab и отбрасывая ab каналы оставлять только освещенность.

Постановка задачи и модель

Итак у нас есть черно-белое изображение $X \in \mathbb{R}^{H \times W \times 1}$ наша задача восстановить два цветовых канала, т.е. обрести некоторую функцию ${\cal F}: \mathbb{R}^{H \times W \times 1} \rightarrow \mathbb{R}^{H \times W \times 2},\, \hat Y = {\cal F}(X)$.

Наиболее очевидный подход, тренировать свёрточную сеть используя в качестве штрафа обычную $L_2$-норму:

\[L_2(\hat Y, Y) = \sum_{w,h} \left\|\hat Y_{w,h} - Y_{w,h} \right\|^2_2\]

Однако, авторы указывают, что такая штрафная функция плохо подходит, когда нельзя по типу объекта однозначно определить его цвет (яблоко может быть и зеленым и красным и желтым), и в тренировочном датасете встречаются объекты этого типа разных цветов. Тогда если использовать $L_2$-норму в качестве штрафа то мы натренируем модель выбирать для таких объектов какой-то средний (с точки зрения цветовой плоскости) цвет.

Поэтому авторы предлагают вместо задачи регрессии решать задачу классификации, т.е. для каждого пикселя восстанавливать не пару $(a, b)$ координат в цветовом пространстве, а класс/номер цвета. Для этого авторы разбивают цветовую плоскость $ab$ решеткой с шагом $10$ и для каждой ячейки этой решетки, для которой существует цвет назначают класс. Таким образом у них в палитре получается $Q = 313$ цветов.

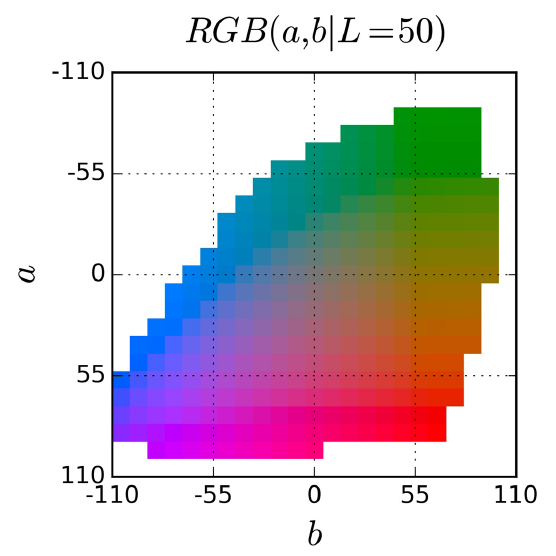
Вместо отыскания функции ${\cal F}$ будем тренировать модель, которая выдаст нам функцию $\hat Z = {\cal G}(X) \in [0, 1]^{H\times W \times Q}$ и уже по $\hat Z$ мы восстановим цвет $\hat Y$ (как именно выясним чуть позже).

Ground-truth, чтобы тренировать такую модель, авторы готовят следующим образом: преобразуют цвет пикселя $Y$ в вектор $Z = {\cal H}^{-1}(Y) \in [0, 1]^{H\times W \times Q}$. Проще всего было бы использовать one-hot кодирование, выбрав в качестве класса ячейку на плоскости ab в которую попал $Y$. Однако, авторы предлагают вместо этого использовать soft-encoding схему. Для этого авторы находят пять ближайших к $Y$ ячеек и выставляют ненулевые значения пропорциональные расстоянию в соответствующие кординаты вектора $Z$.

Для штрафной функции берут мультиклассовую взвешенную кросс-энтропию:

\[L(\hat Z, Z) = -\sum_{w,h} v(Z_{w,h}) \sum_{q} Z_{w,h,q}\ln(\hat Z_{w,h,q})\]

здесь $v(Z_{w,h})$ для того, чтобы перекашивать штраф в сторону редко появляющихся цветов.

Веса авторы подбирали исходя из статистики по цветам в тренировочной части ImageNet датасета:

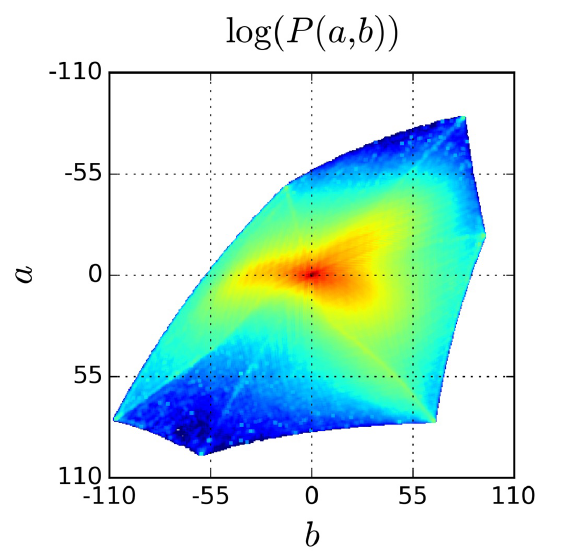
видно, что преобладают “слабораскрашенные” пиксели, и если не перевзвешивать штраф, то после тренировки, модель также будет выдавать “приглушенный” цвет.

Еще набор картинок со статистикой для разных значений $L$ канала:

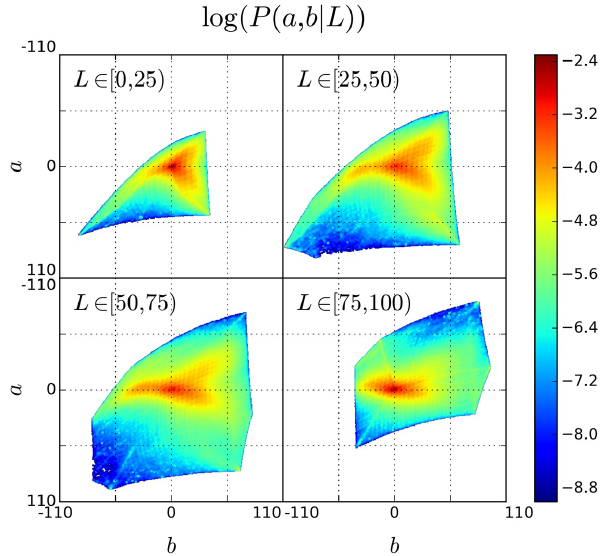
Следующий вопрос, как получив от модели $\hat Z$ восстановить $\hat Y$ в пространстве ab. Есть два очевидных крайних варианта: выбирать цвет (координаты в ab) из класса с наибольшей вероятностью, либо брать взвешенную сумму цветов используя вероятности, полученные от сети в качестве весов. Авторы предлагают следующее:

\[{\cal H}(Z_{w,h}) = \mathbb{E}[f_T(Z_{w,h})],\, f_T(z) = \frac {\exp(\ln(z) / T)} {\sum_q \exp(\ln(z_q) / T)}\]

здесь $T$ - температура выступает гиперпараметром, при $T=1$ у нас будет вариант с взвешенным усреднением, при $T\rightarrow\infty$ - вариант с выбором наиболее вероятного цвета.

Пример результата с разной температурой:

Авторы предлагают выбирать температуру $T=0.38$.

Результаты

Для оценки результатов, авторы используют “тест Тьюринга для раскрашивания”. Они показывают пары: исходную цветную картинку и восстановленную, людям и предлагают определить, которая из них настоящая. Максимальная возможная оценка тут 50% - когда фактически выбор будет равновероятным. Для подхода реализованного авторами качество 32.3%. Правда стоит отметить, что нижняя оценка условий эксперимента, которую авторы получили, прикрепляя к черно-белому изображению цветовые каналы от случайно выбранного другого изображения 13.0%.

Авторы на этом не остановились и провели еще несколько экспериментов, которые могут быть использованы как косвенные оценки качества раскрашивания.

Первый эксперимент. Берем VGG сетку натренированную на неиспорченной тренировочной части ImageNet (VGG - потому что статья 2016 года). Проверяем её на тестовой части получаем 68.3% качества. Обесцвечиваем изображения из тестовой части, прогоняем VGG - получаем 52.7%. Восстанавливаем цвет при помощи подхода, описанного в статье, прогоняем VGG - получаем 56.0%. Т.е. качество выросло относительно черно-белого варианта картинок, но не достигло качество “натурального раскрашивания”. Так же авторы дотренировывают VGG на черно-белых картинках и пишут, что тогда качество (на черно-белых картинках) поднимается до 63.5%.

На самом деле тут не вполне понятно. Т.е. с одной стороны выглядит так, что цвет доставляет только 5% качества, но при этом классификационная сеть тренирующаяся на цветных изображениях сильно на цвет закладывается (теряет 15%).

Второй эксперимент, наиболее интересен и связан с направлением обучения без учителя (self-supervised learning)

Self-supervised обучение

В дополнение к решению собственно задачи раскрашивания, авторы оценивают насколько хорошие признаки научается выделять сетка. Можно считать, что в задаче тренируется автоэнкодер, который по одному из каналов изображения восстанавливает два других, т. е. чтобы расскрасить траву в зеленый цвет, он должен для начала эту траву классифицировать и натренировать для этого такие свёрточные слое, которые выделяли бы хорошие признаки.

Чтобы это проверить, авторы берут AlexNet в качестве базовой модели и тренируют ее для задачи раскрашивания, по схеме, описанной выше, потом берут признаки с каждого слоя и тренируют на них линейные классификаторы. В качестве базовых моделей для сравнения они тренируют AlexNet на задачу классификации на цветных и черно-белых изображениях.

Если я правильно интерпретировал графики из статьи, то AlexNet, который тренировался на классификацию выигрывает с большим отрывом. Вариант для черно-белых изображений даёт +12% к линейному классификатору на признаках от сети раскрашивания, вариант для цветных - +20%.

Правда тут есть пара замечаний. Во-первых, AlexNet не самая приемистая сеть, т.е. можно взять что-то пожирнее и возможно результаты там разойдутся больше, но качество при этом поднимется (но мы помним, что это 2016 год). Во-вторых, не понятно почему авторы ограничиваются тренировкой на ImageNet, очевидно, что весь смысл self-supervised подхода в том, что ему не нужен размеченный датасет и тренироваться можно на произвольном объеме данных.

Второе замечание правда не вполне корректно, авторы решали другую задачу и на self-supervised смотрели как на нечто факультативное.

В заключении картинка. Авторы применили свою модель к исходно черно-белым фотографиям. Результаты, как мне кажется вполне приличные.